But right now, I want to use a specific part Dr. Rockoff's presentation to address a very serious problem with the entire notion of test-based teacher accountability. Keep in mind that Rockoff talks about Student Growth Percentiles (SGPs), but the problem extends to just about any use of Value-Added Modeling (VAM) in teacher evaluation based on test scores. Go to 1:07 in the clip:
The key element here that distinguishes Student Growth Percentiles from some of the other things that people have used in research is the use of percentiles. It's there in the title, so you'd expect it to have something to do with percentiles. What does that mean? It means that these measures are scale-free. They get away from psychometric scaling in a way that many researchers - not all, but many - say is important.
Now these researchers are not psychometricians, who aren't arguing against the scale. The psychometricians as who create our tests, they create a scale, and they use scientific formulae and theories and models to come up with a scale. It's like on the SAT, you can get between 200 and 800. And the idea there is that the difference in the learning or achievement between a 200 and a 300 is the same as between a 700 and an 800.
There is no proof that that is true. There is no proof that that is true. There can't be any proof that is true. But, if you believe their model, then you would agree that that's a good estimate to make. There are a lot of people who argue... they don't trust those scales. And they'd rather use percentiles because it gets them away from the scale.Let's state this another way so we're absolutely clear: there is, according to Jonah Rockoff, no proof that a gain on a state test like the NJASK from 150 to 160 represents the same amount of "growth" in learning as a gain from 250 to 260. If two students have the same numeric growth but start at different places, there is no proof that their "growth" is equivalent.
Now there's a corollary to this, and it's important: you also can't say that two students who have different numeric levels of "growth" are actually equivalent. I mean, if we don't know whether the same numerical gain at different points on the scale are really equivalent, how can we know whether one is actually "better" or "worse"? And if that's true, how can we possibly compare different numerical gains?
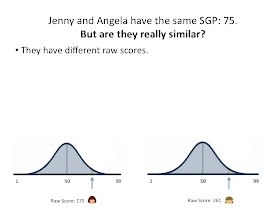
Keep this in mind as we, once again, go through a thought exercise with our friend, Jenny. You may remember from previous posts (here and here) that Jenny is a hypothetical 4th grader who just took the NJASK-4; we're looking to see the implications of Jenny's subsequent SGP. Here's how Jenny "grew" from last year:
Jenny scored a 256 on the NJASK-3 last year, and a 261 on the NJASK-4 this year. She "grew" 5 points over the year (keep in mind that, because the 4th grade test is "harder" than the 3rd grade test, a student can "grow" even if her score drops).
Because she scored a 256 in 3rd grade, Jenny was placed in a group of her peers to calculate her SGP; they all also scored a 256 last year. How did they do?*
Let's note a couple of things: first, the distribution of growth is not what statisticians would call "normal." The distance between Jenny and Julio is only 5 points; the distance between Brittney and Susie is 38 points. But remember also what Rockoff implied: there's no way to compare those two differences. It may well be that it's "easier" to move from Brittney's spot to Susie's than it is to move from Jenny's to Julio's - we just don't know.
Let's look at another student: Angela, who scored a 150 last year. How did she do?
Angela improved her score by 25 points. That sounds wonderful... until we think about what Rockoff said: we can't compare Angela's 25 point gain to someone else, like Jenny, who started in a different place.
Let's look at Angela's "peers":
The range of Angela's cohort is greater than Jenny's: 60 points, as opposed to 50 points for Jenny's "peers." And the distributions are different: look at the differences in growth between the different percentiles in each cohort. Jenny was only 5 points away from the top in her group (there may be a ceiling effect), but Angela is 25 points away from the highest score of her peers.
Here's the thing: let's assume that Angela and Jenny have the median SGPs for their classes. In that case, their SGPs have determined that Angela and Jenny "grew" the same amount for the purposes of evaluating their teachers. Which begs a question:
Is it at all accurate to say that Jenny and Angela "grew" the same amount - and, consequently, that their teachers are equally effective? Well...
They have different raw scores, so we know they are not at the same level of achievement.
Each "grew" a different numeric amount on their scores. But if they "grew"the same amount, remember what Rockoff said: there is no proof that those would represent the same amount of learning. In the same way, we have no proof these different scores represent equivalent amounts of learning.
The SGPs are saying Angela and Jenny "grew" the same amount. But we have no proof that this is true! And not only that...
The SGP hides the different distances from the top, the bottom, and every other position in the distribution for both girls. Which I guess doesn't matter, because the measures can't be compared anyway!
Which leaves us here:
The SGP tells us only one thing: where Jenny and Angela are in relationship to their "peers" when everyone is forced into a normal distribution. But look at all the information that's hidden:
- The raw score, or achievement levels.
- The numeric growth.
- The "actual" growth in learning.
- The range of growth within the group of peers.
- The distribution of growth within the peers.
And yet, even though the SGP tells us nothing about all of this information, the NJDOE (substitute your reformy state education department) confidently tells us that Jenny's and Angela's teachers are equally effective. Perhaps they believe this because they think SGPs "get away from the scales."
Except it's clear they don't do this at all - they just create another scale that is just as suspect. More to come...
* Dopey math error in this graphic has been fixed. Who wants to be my editor? 'Cause the pay is SO awesome...









Two students with the same SGP didn't grow the 'same' amount - what is the same is how their growth compared to their peers.
ReplyDeleteIf the data shows that it is really difficult to boost the achievement of, say, 7th grade students with a prior NJASK score of 170, but that students with a prior NJASK score of 210 show a lot of growth, you would want that to be reflected in any analysis of how their teachers did. The teacher with a lot of students with prior NJASK score of 170 might show less absolute improvement in NJASK scale points, but relative to the typical growth of students with that prior achievement profile, the teacher's performance could be very impressive.
That's what SGPs do for you. They're not perfect. But they're one step closer towards talking about meaningful growth for all students.
Unfortunately, when you characterized SGP you asked the wrong questions.
ReplyDelete"You say Jenny and Angela have the same SGP: 75. But, are they really similar?"
SGP isn't answering that question and can't answer that question. It answers the question, "In comparison to academic peers (students who scored the same in the past), how much did a student grow? Angela and Jenny got an SGP of 75 so they both grew more than 75% of their academic peers.
When estimating the impacts of teachers, if Mrs. Jones consistently moved students at a rate greater than 75% of each student's peers then that teacher did a great job. SGP doesn't assume all students starts at the same place at the start of the school year.
Make sure you understand the question being answered by SGP! Your analysis misrepresents what SGP tells us.
And, the scales created my some test publishers may be vertically aligned but the change in points per question is a U-shaped function. Going from 0 questions right last year to 1 questions right this year may be an increase along the scale of 150 points, but moving from 20 to 21 questions would be 7 points. Given your argument, would the first student have learned 20x more than the second student? I think not.
alm and Jim:
ReplyDeleteI fully understand what an SGP tells us, and I don't think I misrepresent them at all here. My point is that what an SGP tells us is not good enough to evaluate a teacher.
alm, you say that students in different parts of the test scale will likely grow differently. That's absolutely true, but using SGPs does not solve that issue. There is no proof that two students at different levels who grew different numeric amounts, yet have the same SGP, grew in "actual" learning the same amount. Just because they fall in the same place in a forced normal distribution of their peers doesn't mean they had equivalent real growth. Consequently, there's no evidence their teachers were equally "effective."
(That puts aside the whole question of whether a descriptive measure like SGPs can attribute growth to teachers anyway.)
Jim, I think you're making my point. SGPs cannot tell us what we really need to know: whether two students at different parts of the test scale grew in "real" learning the same amount. I understand fully the question SGPs are asking; again, I don't think I misrepresented that at all. My point is that it's an irrelevant question with regards to evaluating teachers. Your point about U-shaped scaling actually bolsters my contention: SGPs cannot tell us that growth at one part of the scale is equivalent to growth at another part.
And yet, that's exactly what they purport to do. If Angela and Jenny are the median students in their classes, the NJDOE says their teachers are equivalently effective.
There simply no reason to believe that's true.
Very interesting stuff Jazzman!
ReplyDeleteAnd here's a "right" question to ask! What are original "raw" scores? As there are times when the "raw" scores get "cleaned up".
So if the scores are used for evaluation purposes, everyone should be entitled to the original raw scores and the "cleaned up" raw scores.
>Consequently, there's no evidence their teachers were equally "effective."
ReplyDeleteI think you are trying to have it two ways here - the measure you seem to be asking for (the same 'amount' of learning) is, if I'm reading you correctly, basically unadjusted student growth (increase in raw points, maybe).
But you DEFINITELY don't want a system that uses raw gains to compare teachers across different grades (and who teach relatively higher/lower performing students). The reason that you do a forced normal distribution is to account for systematic differences in variance for different grade levels, prior levels of achievement, etc.
Here's how I would describe it -- any assessment score is a proxy for some latent trait that you're trying to measure. The supposition is that change in the score represents change in the latent measure. I'm not sure what would constitute 'proof' for you - there's a process by which any scaled assessment instrument gets put through its paces -- not sure that a blog comment is the right place to get into the philosophy of measurement, but there's a sound and accepted body of practice here, and it sounds like that's what you have issue with - not NJ's SGP's per se.
But let's bring it back to the question: what does a teacher whose students have high SGP tell us?
Well, you want to know if it is consistent, for one. So you probably want to look at several years of data. And if that's all over the place, the SGP isn't telling you a lot.
But if the score is consistently high -- or consistently low -- that, taken in context with the totality of other things you know about the teacher might give you some insight about how to make promotion, compensation or hiring decisions, given an environment of limited resources.
I'm skeptical of a LOT of the policy around this, too. Mike Petrilli from the Fordham Institute was really critical of these state-mandated eval systems in a recent podcast - his basic point (which I agree with) is that it is difficult to impossible to come up with an evaluation formula that applies across every school and every teaching position.
What you probably need to do is give the best information possible to local decisionmakers -- principals! to make staffing decisions. Which, yes, includes hiring and firing. But when I say good information I also mean information about the limits of these instruments. There is a frightening level of innumeracy in the education profession, and it unfortunately extends to the principal's office in many situations.
The only way that you'll have this information used coherently for 5th grade math teachers, Art teachers and Phys Ed teachers is if you let principals make decisions. But you can't have this both ways -- authority to hire & fire is still a 3rd rail issue in labor contracts, but it's basically a prerequisite if your primary goals are to create a system where:
-student achievement is job #1
-schools are staffed with the best teachers out there
-information gets used in a sensible way.
So to be clear, I don't think that this is being handled the right way -- you are right to raise issues with one-sized-fits-all eval schemes -- but inside the current system of highly scripted, formalized evaluation schemes, with appeals and grievance committees, etc. etc. SGPs are probably the best system you'll find.
alm, SGP's are not "the best system" you'll find to evaluate teacher effects. A MAJOR threat to validity is maturation effects. The students get older therefore their changes cannot be attributed to teacher effects. No honest researcher, given this data and lack of experimental control would make the claim that SGPs measure teacher induced changes.
ReplyDeleteJazzman just pointed out that the relationship between scores and teacher effects are INVALID due to misinterpretation of relative growth scores. Given these major control problems using SGP's tells us nothing. What part of INVALID don't you get?
When May 15th passed w/o a pink slip for me I thought Camden BOE had missed its window of opportunity. But the Rice Notice of their intent to do just that was hand delivered yesterday. Apparently, as the boys from the state pored over the files looking for unsuspecting mooks they missed in the first pass, they found me. I can imagine how they shouted out with glee when they found a 13 year veteran NJEA member STILL one day short of tenure!
ReplyDeleteHowever, when I googled pink slips for untenured Camden teachers, I learned it was MY responsibility to notify the board in writing by June 1, that I had accepted continued employment, when I'd received nothing at all from the BOE by May 15 deadline. (Yes you read that right).
But I will have the last laugh. If the boys from the state think that I won't hand them the flag untenured teachers have been carrying FOR YEARS against NJEA policies like this one, I've got news for them. When it comes to stealing my paycheck for rendering no service in return, you fellas have met your match in the NJEA.