Let's suppose you and I get jobs digging holes. Let's suppose we get to keep our jobs based on how well we dig
relative to each other.
It should be simple to determine who digs more: all our boss has to do is measure how far down our holes go. It turns out I'm much better at digging than you are: my holes are deeper, I dig more of them, and you can't keep up.
The boss, after threatening you with dismissal, sends you over to my job site so you can get
professional development on hole digging. That's where you learn that, while you've been using a hand shovel, I've been using a 10-ton backhoe. And while you've been digging into bedrock, I've been digging into soft clay.
You go back to the boss and complain about two things: first, it's wrong for you and me to be compared when the circumstances of our jobs are so different. Second, why is the boss wasting your time having me train you when there's nothing I can teach you about how to do your job?
The boss has an answer: he is using a statistical method that "
fully takes into account" the differences in our jobs. He claims there's no bias against you because you're using a shovel and digging into rock. But you point out that your fellow shovelers consistently get lower ratings than the workers like me manning backhoes.
The boss argues back that this just proves the shovelers are worse workers than the backhoe operators. Which is why you need to "learn" from me, because "all workers can dig holes."
Everyone see where I'm going with this?
* * *
There is a debate right now in New Jersey about how Student Growth Percentiles (SGPs) are going to be used in teacher evaluations. I've
written about SGPs here
many times (one of my latest is
here), so I'll keep this recap brief:
An SGP is a way to measure the "growth" in a student's test scores from one year to the next,
relative to similar students. While the actual calculation of an SGP is complicated, here's the basic idea behind it:
A student's prior test scores will predict their future performance: if a student got low test scores in Grades 3 through 5, he will probably get a low score in Grade 6. If we gather together all the students with similar test score histories and compare their scores on the latest test, we'll see that those scores vary: a few will do significantly better than the group, a few will do worse, and most will be clustered together in the middle.
We can rank and order these students' scores and assign them a place within the distribution; this is, essentially, an SGP. But we can go a step further: we can compare the SGPs from one group of students with the SGPs from another. In other words: a student with an SGP of 50 (SGPs go from 1 to 99) might be in the middle of a group of previously high-scoring students, or she might be in the middle of a group of previously low scoring students. Simply looking at her SGP will not tell us which group she was placed into.
To make an analogy to my little story above: you and I might each have an SGP of 50. But there's no way to tell, solely based on that, whether we are digging into clay or bedrock. And there's no way to tell from a students' SGP whether they score high, low, or in the middle on standardized tests.
And this is where we run into some very serious problems:
The father of SGPs is Damian Betebenner, a widely-respected psychometrician. Betebenner has written several papers on SGPs; they are highly technical and well beyond the understanding of practicing teachers or education policymakers (not being a psychometrician, I'll admit I have had to work hard to gain an understanding of the issues involved).
Let's start by first acknowledging (and as
Bruce Baker pointed out years ago) that
Betebenner himself believes that SGPs do not measure a teacher's contribution to a student's test score growth. SGPs, according to Betebenner, are
descriptive; they do not provide the information needed to say
why a student's scores are lower or higher than prediction:
Borrowing concepts from pediatrics used to describe infant/child weight and height, this paper introduces student growth percentiles (Betebenner, 2008). These individual reference percentiles sidestep many of the thorny questions of causal attribution and instead provide descriptions of student growth that have the ability to inform discussions about assessment outcomes and their relation to education quality. A purpose in doing so is to provide an alternative to punitive accountability systems geared toward assigning blame for success/failure (i.e., establishing the cause) toward descriptive (Linn, 2008) or regulatory (Edley, 2006) approaches to accountability.(Betebenner, 2009) [emphasis mine]
This statement alone is reason enough why New Jersey should
not compel employment decisions on the basis of SGPs:
You can't fire a teacher for cause on the basis of a measure its inventor says does not show cause.
It's also important to note that SGPs are
relative measures. "Growth" as measured by an SGP is not an absolute measure; it's measured in relationship to other, similar students. All students could be "growing," but an SGP, by definition, will always show some students growing below average.
But let's put all this aside and dig a little deeper into one particular matter:
One of the issues Betebenner admits is a problem with using SGPs in teacher evaluation is a highly technical issue known as
measurement endogeneity; he outlines this problem in a paper he coauthored in 2015(2) --
well after New Jersey adopted SGPs as its official "growth" measure.
The problem occurs because test scores are error-prone measures. This is just another way of saying something we all know:
test scores change based on things other than what we want to measure.
If a kid gets a lower test score than he is capable of because he didn't have a good night's sleep, or because he's hungry, or because the room is too cold, or because he gets nervous when he's tested, or because some of the test items were written using jargon he doesn't understand, his score is not going to be an accurate representation of his actual ability.
It's a well-known statistical precept that variables measured with error tend to bias positive estimates in a regression model downward, thanks to something called
attenuation bias. (3) Plain English translation:
Because test scores are prone to error, the SGPs of higher-scoring students tend to be higher, and the SGPs of lower-scoring students tend to be lower.
Again: I'm not saying this; Betebenner --
the guy who invented SGPs -- and his coauthors are:
It follows that the SGPs derived from linear QR will also be biased, and the bias is positively correlated with students’ prior achievement, which raises serious fairness concerns....
The positive correlation between SGP error and latent prior score means that students with higher X [prior score] tend to have an overestimated SGP, while those with lower X [prior score] tend to have an underestimated SGP. (Shang et al., 2015)
Again, this means we've got a problem at the student level with SGPs: they tend to be larger than they should be for high-scoring students, and lower than they should be for low-scoring students. Let me also point out that Betebenner and his colleagues are the ones who, unprompted, bring up the issue of "fairness."
Let's show how this plays out with New Jersey data. I don't have student-level SGPs, but I do have school-level ones, which should be fine for our purposes.
If SGPs are biased, we would expect to see high-scoring schools show higher "growth," and low-scoring schools show lower "growth." Is that the case?
New Jersey school-level SGPs are biased exactly the way its inventor predicts they would be -- "which raises serious fairness concerns."
I can't overemphasize how important this is.
New Jersey's "growth" measures are biased against lower-scoring students, not because their "growth" is low, but likely because of inherent statistical properties of SGPs that make them biased. Which means they are almost certainly going to be biased against the teachers and schools that enroll lower-scoring students.
Shang et al. propose a way to deal with some of this bias; it's highly complex and there are tradeoffs. But we don't know if this method has been applied to New Jersey SGPs in this or any other year (I've looked around the NJDOE website for any indication of this, but have come up empty).
In addition: according to Betebenner himself, there's another problem when we look at the SGPs for a group of students in a classroom and attribute it to a teacher.
You see, New Jersey and other states have proposed using SGPs as a way to evaluate teachers. In its
latest federal waiver application, New Jersey stated it would use median SGPs (mSGPs) as a way to assess teacher effectiveness. This means the state looks at all the scores in a classroom, picks the score of the student who is right in the middle of the distribution of those scores, and attributes it to the teacher.
The problem is that
students and teachers are NOT randomly assigned to classrooms or schools. So a teacher might pay a price for teaching students with a history of getting lower test scores. Betebenner et al. freely admit that their proposed correction -- and again, we don't even know if it's currently being implemented -- can't entirely get rid of this bias.
As we all know, there is a clear correlation between test scores and student economic status. Which brings us to our ultimate problem with SGPs:
Are teachers who teach more students in poverty unfairly penalized when SGPs are used to evaluate educator effectiveness?
I don't have the individual teacher data to answer this question. I do, however, have school-level data, which is more than adequate to at least address the question initially. What we want to know is whether SGPs are correlated with student characteristics. If they are, there is plenty of reason to believe these measures are biased and, therefore, unfair.
So let's look at last year's school-level SGPs and see how they compare to the percentage of free lunch-eligible students in the school, a proxy measure for student economic disadvantage. The technique I'm using, by the way, follows Bruce Baker's work
year after
year, so it's not like anything I show below is going to be a surprise.
SGPs in math are on the vertical or y-axis; percentage free lunch (FL%) is on the horizontal or x-axis. There is obviously a lot of variation, but the general trend is that as FL% rises, SGPs drop.
On average, a school that has no free lunch students will have a math SGP almost 14 points higher than a school where all students qualify for free lunch. The correlation is highly statistically significant as shown in the p-value for the regression estimate.
Again: we know that, because of measurement error, SGPs are biased against low-scoring students/schools. We know that students in schools with higher levels of economic disadvantage tend have lower scores. We don't know if any attempt has been made to correct for this bias in New Jersey's SGPs.
But we do know that even if that correction was made, the inventor of SGPs says: "
We notice the fact that covariate ME correction, specifically in the form of SIMEX, can usually mitigate, but will almost never eliminate aggregate endogeneity entirely." (Shang et al., p.7)
There is more than enough evidence to suggest that SGPs are biased and, therefore, unfair to teachers who educate students who are disadvantaged. Below, I've got some more graphs that show biases based on English language arts (ELA) SGPs, and correlations with other student population characteristics.
I don't see how anyone who cares about education in New Jersey -- or any other state using SGPs -- can allow this state of affairs to continue.
Despite the assurances of previous NJDOE officials, there is more than enough reason for all stakeholders to doubt the validity of SGPs as measures of teacher effectiveness.
The best thing the Murphy administration and the Legislature could do right now is to tightly cap the weighting of SGPs in teacher evaluations. This issue
must be studied further; we can't force school districts to make personnel decisions on the basis of measures that raise "
...serious fairness concerns..."
Minimizing the use of SGPs is the only appropriate action the state can take at this time. I can only hope the Legislature, the State BOE, and the Murphy administration listen.
SCATERPLOTS:
Here's the correlation between ELA-SGPs and FL%. A school with all FL students will, on average, see a drop of more than 9 points on its SGP compared to a school with no FL students.
Here are correlations between SGPs and the percentage of Limited English Proficient (LEP) students. I took out a handful of influential outliers that were likely the result of data error. The ELA SGP bias is not statistically significant; the math SGP bias is.
There are also positive correlations between SGPs and the percentage of white students.
Here are correlations between students with disabilities (SWD) percentage and SGPs. Neither is statistically significant at the traditional level.
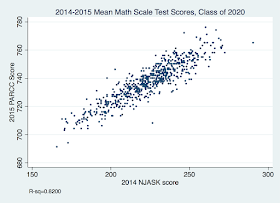
Finally, here are the correlations between some grade-level SGPs and grade-level test scores. I already showed Grade 5 math above; here's Grade 5 ELA.
And correlations for Grade 7.
Sources:
1)
Betebenner, D. (2009). Norm- and Criterion-Referenced Student Growth. Educational Measurement: Issues and Practice, 28(4), 42–51. https://doi.org/10.1111/j.1745-3992.2009.00161.x
2)
Shang, Y., VanIwaarden, A., & Betebenner, D. W. (2015). Covariate Measurement Error Correction for Student Growth Percentiles Using the SIMEX Method. Educational Measurement: Issues and Practice, 34(1), 4–14. https://doi.org/10.1111/emip.12058
3)
Wooldridge, J. (2010). Econometric Analysis of Cross Section and Panel Data (Second Edition). Cambridge, MA: The MIT Press. p. 81.